W 1904 roku
szwedzki matematyk Helge von Koch skonstruował dziwną figurę,
która z wyglądu przypomina płatek śniegu.
Konstrukcja płatka śniegu
Krok pierwszy
Rysujemy trójkąt równoboczny o długości
boku np. 1. Każdy bok trójkąta dzielimy na trzy równe części
i doklejamy do części środkowej, tak jak na rysunku, trójkąt
równoboczny o boku trzy razy krótszym. Z trójkąta powstała
12 boczna gwiazda. Każdy jej bok ma długość równą
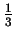 . .
Krok drugi
Każdy bok gwiazdy dzielimy znowu na trzy
równe części i do części środkowej doklejamy trójkąt
równoboczny o boku trzy razy krótszym niż poprzednio.
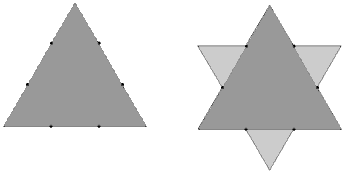
Otrzymamy 48 boczną gwiazdę o długości boku
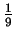 . .

Kolejne kroki
W kolejnych krokach postępujemy podobnie
jak poprzednio. W trzecim kroku powstanie gwiazdka, która ma
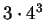 jednakowej długości boków. Rysunek poniżej pokazuje gwiazdkę
po 5 krokach konstrukcji. Gwiazdka ta ma
jednakowej długości boków. Rysunek poniżej pokazuje gwiazdkę
po 5 krokach konstrukcji. Gwiazdka ta ma
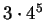 , czyli
3072 boki. , czyli
3072 boki.

|
|
|
Krzywa Kocha
|
W 1905 roku włoski matematyk
Ernesto Cesaro zachwycony
wewnętrzną nieskończonością
krzywej Kocha napisał o niej:
Gdyby była obdarzona
życiem, można by się jej
pozbyć tylko niszcząc ją w
całości. W przeciwnym razie
odżywałaby znowu i znowu, z
głębi swych trójkątów, tak
jak czyni to życie we
Wszechświecie.
|
|
|
|
Konstrukcję tę możemy powtarzać dowolnie wiele razy. Z powodu
ograniczonej rozdzielczości ekranu oraz oka następne obrazki
nie będą się już wiele różniły od tego co zobaczyliśmy po 5
krokach. Co się dalej będzie działo możemy już sobie tylko
wyobrażać. A jak będzie wyglądała taka 'graniczna' gwiazda
po wykonaniu nieskończenie wielu kroków? Okazuje się, że
jest to figura o trudnych do wyobrażenia własnościach.
Nazywamy ją płatkiem śniegu, a jej brzeg
krzywą Kocha.
Płatek śniegu, chociaż powstał z sumowania nieskończenie
wielu trójkątów, ma skończone pole. Jego brzeg jest bardzo
dziwną krzywą. Ta krzywa ma nieskończoną długość, choć jak
mogliśmy to sprawdzić, ogranicza obszar o skończonym polu.
Trudno to sobie wyobrazić, ale ta krzywa nie zawiera żadnych
odcinków - w każdym swym punkcie ma 'zagięcie', a więc w
żadnym swym punkcie nie ma stycznej.
|