Ten dział przeznaczony jest nie tylko dla tegorocznych maturzystów, ale dla każdego, kto chciałby sprawdzić swoją wiedzę już dziś. Nawet pierwszoklasista może spróbować rozwiązywać arkusz podstawowy z maja 2003 roku. Zadania pochodzą ze strony Centralnej Komisji Egzaminacyjnej : www.cek.edu.pl

EGZAMIN MATURALNY Z MATEMATYKI
POZIOM PODSTAWOWY
 
Arkusz I
Czas pracy 120 minut
Za rozwiązanie wszystkich zadań można otrzymać łącznie 40 punktów.

• Zadanie 1. (4pkt.)
Lewa strona równania jest sumą nieskończonego ciągu geometrycznego o ilorazie . Z rachunku zbieżności mamy . Zatem dziedziną równania jest przedział (-1,1).
Równanie można zapisać w postaci . Stąd .
Pierwiastkami ostatniego równania są liczby : należące do dziedziny.
Odpowiedź : Rozwiązaniami równania są liczby .
Postępójąc w analogiczny sposób rozwiąż równanie : .

• Zadanie 2. (4pkt.)
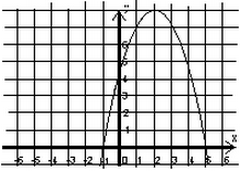
Rysunek przedstawia fragment wykresu funkcji kwadratowej ƒ.
a) Podaj miejsca zerowe funkcji ƒ.
b) Podaj rozwiązania nierówności ƒ(x)≤0.
c) Podaj rozwiązania równania ƒ(x)=3.

• Zadanie 3. (4pkt.)
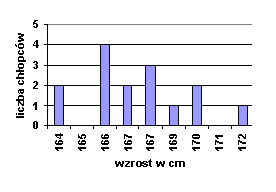
Dane dotyczące wzrostu chłopców z klasy II B przedstawione są na diagramie.
a) Oblicz średnią wzrosty chłopców z klasy II B (podaj wynik dokładny).
b) Ilu chłopców z klasy II B ma wzrost wyższy od średniego?

• Zadanie 4. (3pkt.)
Liczby 102, 105, 108, 111, ... są kolejnymi wyrazami pewnego ciągu arytmetycznego. Zapisz wzór na n-ty wyraz tego ciągu. Oblicz wyraz .

• Zadanie 5. (5pkt.)
Przed wejściem do przychodni lekarskiej znajdują się schody mające 8 stopni po 15 cm wysokości każdy. Postanowiono zbudować podjazd dla niepełnosprawnych o nachyleniu 7°. Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm.

• Zadanie 6. (3pkt.)
Ciąg określony jest wzorem

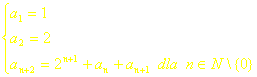
Wyznacz czwarty wyraz tego ciągu.

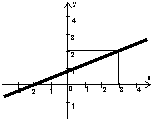• Zadanie 7. (5pkt.)
Rysunek przedstawia fragment wykresu funkcji liniowej ƒ. Wykres funkcji g jest obrazem wykresu funkcji ƒ otrzymanym za pomocą przesunięcia o wektor . Wyznacz miejsce zerowe funkcji g.

• Zadanie 8. (3pkt.)
Składka na ubezpieczenie zdrowotne jest równa 7,5% podstawy wymiaru składek na ubezpieczenie społeczne. Podstawa wymiaru składek na ubezpieczenie społeczne jest równa 60% przeciętnego wynagrodzenia. Oblicz wysokość składki na ubezpieczenie zdrowotne przyjmując, że przeciętne wynagrodzenie jest równe 1869,76 zł. Wynik podaj w zaokrągleniu do 1 grosza.

• Zadanie 9. (3pkt.)
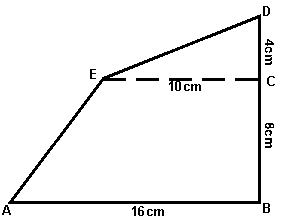
Oblicz pole działki rekreacyjnej, której plan przedstawiony jest na rysunku. Zakładamy że kąty ABC i ECD są kątami prostymi.

• Zadanie 10. (2pkt.)
Kupując los loterii można wygrać nagrodę główna, którą jest zestaw płyt kompaktowych lub jedną z 10 nagród książkowych. Przy zakupie jednego losu prawdopodobieństwo wygrania nagrody książkowej jest równe . Oblicz ile jest losów pustych.

• Zadanie 11. (4pkt.)
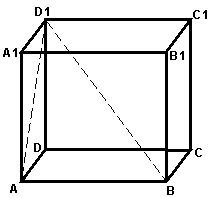
Podstawą prostopadłościanu jest prostokąt o bokach długości : i . Wysokość prostopadłościanu ma długość równą 6. Uzasadnij, za pomocą rachunków, że trójkąt jest prostokątny.